A swimming pool is a popular amenity in the South Texas climate. Whether or not a rainwater system can support one depends on the capacity of the rainwater system and the amount of water to be used for the pool.
In the discussion that follows, we will assume that rainwater is to be the sole source of water for the pool. However, it's important to remember that this need not be the case -- it may be expedient and economical to share collected rainwater with other sources.
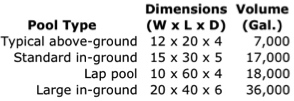
Filling the PoolIf rainwater is to be the sole source of water for an existing pool, storage must be sufficient to tolerate use of thousands of gallons when the pool is filled (or refilled). The table below gives approximate volumes for pools of a few common dimensions (in feet). Depth is estimated as an average of the deepest and shallowest depths.

These amounts are likely to represent a substantial proportion of most rainwater storage tanks, although timing pool filling during the wetter months may prevent tank levels from falling dangerously low, since these are the times when tanks are likely to fill to capacity and water otherwise is lost to overflow. But if filling a pool from storage is not an option, traditional sources such as municipal or well water makes good sense. Also, many pool maintenance companies will fill pools from tank trucks.
Evaporative Loss
Once the pool is filled, a rainwater system must be capable of supporting replacement of water lost to evaporation. In addition to evaporation, there may be other sources of loss such as leakage or enthusiastic splashing. The discussion here is limited to evaporation -- it may or may not be possible to control these other losses, but evaporative loss is inevitable and will require constant replenishment.
The amount of evaporative loss is largely a function of surface area, although air and water temperature, relative humidity, surface wind velocity, and solar radiation have their effect. Quantities of water lost may seem minor compared to total pool volume, but evaporation is continuous and amounts add up over the course of months, particularly during the swimming season when temperatures are at their highest and rainfall is infrequent.
Predicting the amount of evaporative loss precisely would depend on detailed local climatological knowledge. An estimate can be made by filling a container and keeping track of the water level over a period of time. This may not give a good prediction of water loss in a pool however, since its smaller volume and depth are likely to result in exaggerated variation in water temperature. Actual measurements on an existing pool can give a good idea about amounts of water needed to compensate for evaporative loss in a given climatic region.
Water level measurement
One way to estimate evaporative loss is by measuring the drop in water level over some convenient period of time and using this to calculate gallons lost. This is best done during dry periods, as it can be tricky compensating for increases in level due to rain.
Gallons lost = (Surface area in square feet) x (Drop in level in inches) x 0.6234*
* 0.6234 is the amount in gallons of a volume 12 x 12 x 1 inches.
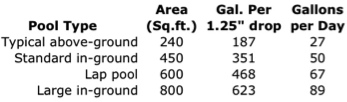
For example, a 1.25 inch drop in level of a typical above-ground pool (240 square feet in surface area) would result in:
240 x 1.25 x 0.6234 = 187.01 gallons
Dividing this volume by the length of time during which the drop in level ocurred gives a rate that can be used to estimate future evaporative loss. If, in this example, the 1.25 inch drop occurred over a week, the daily evaporation loss would be about 27 gallons. To make this more general, we calculate a daily Evaporation Rate (gallons lost per square foot of surface area per day) of 27/240 = 0.1125.
The table below gives examples of loss associated with a 1.25" drop in water level (Evaporation Rate = 0.1125) for pools of different sizes. the Gallons per Day column assumes that the drop occurred over a week's time.
Direct measurement
Another way to estimate the effects of evaporation is by direct measurement of the water required to compensate for loss. This too is simpler if done during dry weather, although water added from rainfall is easy enough to include if its precise measurement is known, and it does not overflow the pool.
The example here is a small rectangular above-ground masonry pool located near the northern boundary of San Antonio, TX. Pool volume is 6,600 gallons, surface area about 220 square feet. There is no leakage, and water is circulated through a skimmer opening and sub-surface jets -- that is, there are no enhancements such as a fountain or waterfall that would increase evaporation beyond that expected from the water surface alone.
Water was added and measured 24 times over a 128 day period lasting from the end of May 2011 through the end of September. During this time 3,471 gallons, or about 27 gallons per day were added to make up for losses due to evaporation during the swimming season (this included 4 instances of rainfall totalling 2.65 inches or about 370 gallons). This yields an Evaporation Rate of 27/220 = 0.1227, corresponding approximately to a drop in water level of 1.37 inches per week.
In the absence of other data, it is not certain how precisely this evaporation rate might apply to other seasons or other pools in the South Texas area. Factors that elevate the rate are the record high temperatures the summer of 2011, and the location of the pool from which this rate is calculated, high on a southeast-facing hill where there is a nearly constant breeze. On the other hand, air temperatures at this location tend to be 3 - 5 degrees cooler than at lower elevations, and the pool is protected by carefully placed shade sails that reduce direct exposure to the sun during the hottest part of the day (see photo below). Nonetheless, this measure is consistent with anecdotal reports of water loss in other pools during the warmer months.

The Benefit of Evaporative Loss
In spite of the trouble and expense of adding water to compensate for losses due to evaporation, it should be understood that evaporation, or more precisely, evaporative cooling is a critical factor in maintaining a confortable water temperature. It is possible to stop evaporation altogether by covering the pool surface with a plastic pool cover. But aside from the inconvenience, doing this will raise water temperature to uncomfortable levels (90° - 100°F) in an outdoor pool in our summer climate, especially if it is unshaded. We have found that leaving water surface uncovered and arranging shading to reduce direct overhead sunlight by 1/3 to 1/2 leaves water temperature between 82° and 85°F when an equilibrium has been reached between solar heating and evaporative loss between the end of May and the middle of September.
Thus, evaporation is highly beneficial, but evaporative loss must be made up. Depending on rainfall, it may not be necessary to compensate for loss entirely from stored water. But it is best to plan for extended periods of drought and to have storage of sufficient capacity to supply water in the range of amounts shown here.
Some Estimates
The following table illustrates the effect of evaporation over time, giving estimated amounts of loss in gallons per day, week and 120-day season for pools of common dimensions. Because of uncertainties about the exact evaporation rate, calculations are based on four different values (0.10, 0.11, 0.12 and 0.13) that presumably include plausible rates for differing local environments in our area. The last column (%of Volume) expresses total seasonal loss as a proportion of pool volume. Daily loss has been rounded to the nearest whole number.
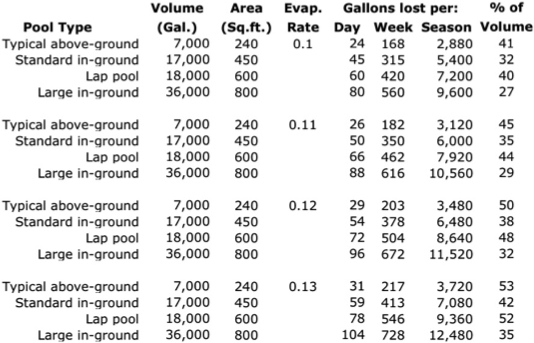
Depending on the evaporation rate and pool dimensions, loss accumulated over a summer season is likely to be in the thousands of gallons, and can approach a significant fraction of pool capacity -- over 50% in the worst case for a typical above-ground pool.
The table also suggests that, for example, a standard 15 x 30 foot in-ground pool can be expected to lose from 45 to 59 gallons per day during the summer months. To put this in perspective, this is as much as, or more than one person's daily water use in a modestly water-conserving household.Planning for a Rainwater-supplied Pool
The first step in establishing rainwater supply requirements is to measure pool dimensions. For an existing pool, volume and surface area measurements can be made quite easily. For a pool or and/or a rainwater catchment system that is to be built, the process is basically the same, although there are likely to be fewer constraints if pool size is not yet fixed. Assuming that there is a water supply (rainwater or other) that is sufficient to fill the pool, the next step is to estimate daily rate of water loss. Water loss may be estimated by either one of the two methods given above. (If the pool has no water-using enhancements and the gallons/square foot/day rate averaged over the season is much higher than 0.13 it may be advisable to investigate the possibility of leaks in the plumbing or walls.)
Gallons lost per season gives a rough idea of the amount of storage needed to replace lost water for a pool of a given size in the absence of rain:
Loss per season = (daily rate) x (pool surface area) x (120 days)
For example, suppose we find a daily evaporation rate of 0.12 gallons/square foot/day in an above-ground pool of 240 square feet of surface area. The pool would lose about 28.8 gallons a day, or0.12 x 240 x 120 = 3,456 gallons per season.
We can use the Rainwater Harvest Estimator to estimate the volume of storage needed to supply replacement water for catchment areas and storage tanks of various sizes. To do this, we start with input parameters as follows:
The goal is to find combinations of catchment areas and storage volumes such that storage does not run out during the swimming season. We do this by systematically changing the Storage volume for various sizes of Catchment area in the Estimator spreadsheet and recording the Number of days tanks are empty values. Catchment areas examined range from 2,000 to 3,000 square feet (common roof areas for U.S. housing), in five increments of 250 square feet. Storage area is varied from 2,500 to 4,000 gallons in four increments of 500 gallons. The graph below summarizes the results:
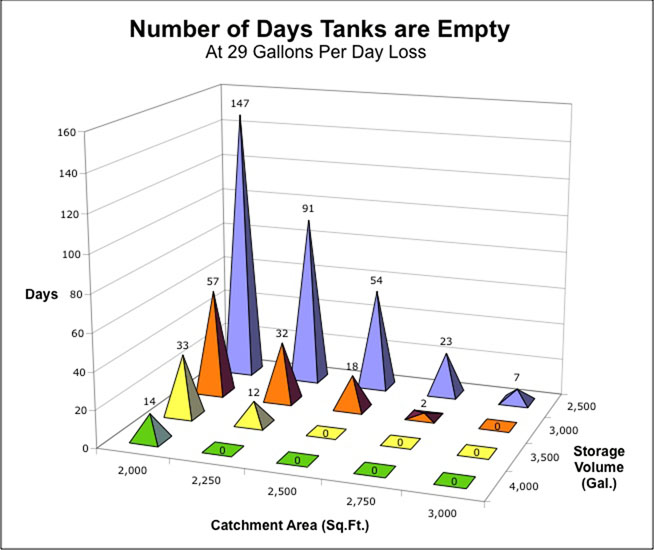
Eight of the combinations of catchment and storage result in zero days of empty tanks, and which potentially could supply enough water to replace loss. But the graph also illustrates some combinations that will not work if rainwater is the sole source. For example, the lowest value for catchment (2,000 square feet) will not supply enough water at any of the storage volume levels. Likewise the smallest tank (2,500 gallons) does not hold enough water to keep from going dry, no matter how much is collected from any of the roof areas shown. Presumably, someone living on property with 2,500 square feet of collection area would want to have at least 3,500 gallons of storage just to be safe.
It may seem extreme to reject combinations that fail for only a few days out of the 30 years of daily climatological records for San Antonio on which the Rainfall Harvest Estimator is based, particularly since the analysis here assumes no rainfall to replenish tanks or to add directly to the pool itself (every inch of rainfall adds an inch to pool water level). However, in instances where there is no alternative to rainwater, it is always wise to plan for the worst case.
With alternate sources of water, these constraints can be lessened somewhat. In fact, with a 2,000 square foot catchment area and 2,000 gallons of storage, storage levels would have been empty only about 275 days out of the 11,000+ daily records in the Estimator database. This suggests that small rainwater systems designed only as supplements to pool maintenance could be an important source for water conservation. Such a system might not avert drought-related municipal restrictions on swimming pools, however, since water shortages are synchronized -- the same 275 days mentioned here occurred at the same time that wells and municipal systems were running short.
Nothing beats a self-sustaining system designed to accommodate the extremes of South Texas weather.
Some Notes on Pool Water Quality
The use of rainwater makes a pool easy to maintain. Its lack of dissolved minerals makes it simple to maintain a neutral pH without the addition of large quantities of acid, and once stabilized, minimal amounts of chlorine-based oxidizer is needed to keep it clear, odorless and free of irritants.
BBB (Bleach, Baking soda and Borax) is simple and effective maintenance method that works particularly well with rainwater. An introduction can be found at the following Web site:
http://www.troublefreepool.com/bbb-for-beginners-t5208.htmlThe Pool Calculator is a useful tool for determining dosages of chemicals required to keep pool water in balance. It can be found at the following Web site:
http://www.poolcalculator.com/It is also available as an iPhone app.
PLEASE NOTE: I have done my best to check the accuracy of the tables and calculations on this page. Further, the conclusions and assertions made are intended as guidelines and may not apply to actual situations. Thus, I must assert the usual disclaimer that the information presented here is distributed without warranty, and that you use it at your own risk.